In the first half of this post, I outlined a solution to Project Euler problem 137 and will continue with the solution here. Stop reading now if you don't want to be spoiled. There was no code in the first post, so this post will be mostly code, providing a pretty useful abstraction for dealing with binary quadratic forms.
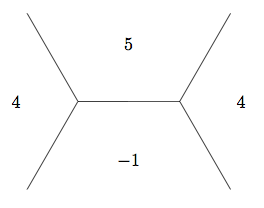
In the very specific solution, I was able to use one picture to completely classify all integer solutions to the equation \(5 x^2 - y^2 = 4\) due to some dumb luck. In the solution, we were able to use "Since every edge protruding from the river on the positive side has a value of 4 on a side...by the climbing lemma, we know all values above those on the river have value greater than 4," but this is no help when trying to find solutions to \(5 x^2 - y^2 = 9\), for example.
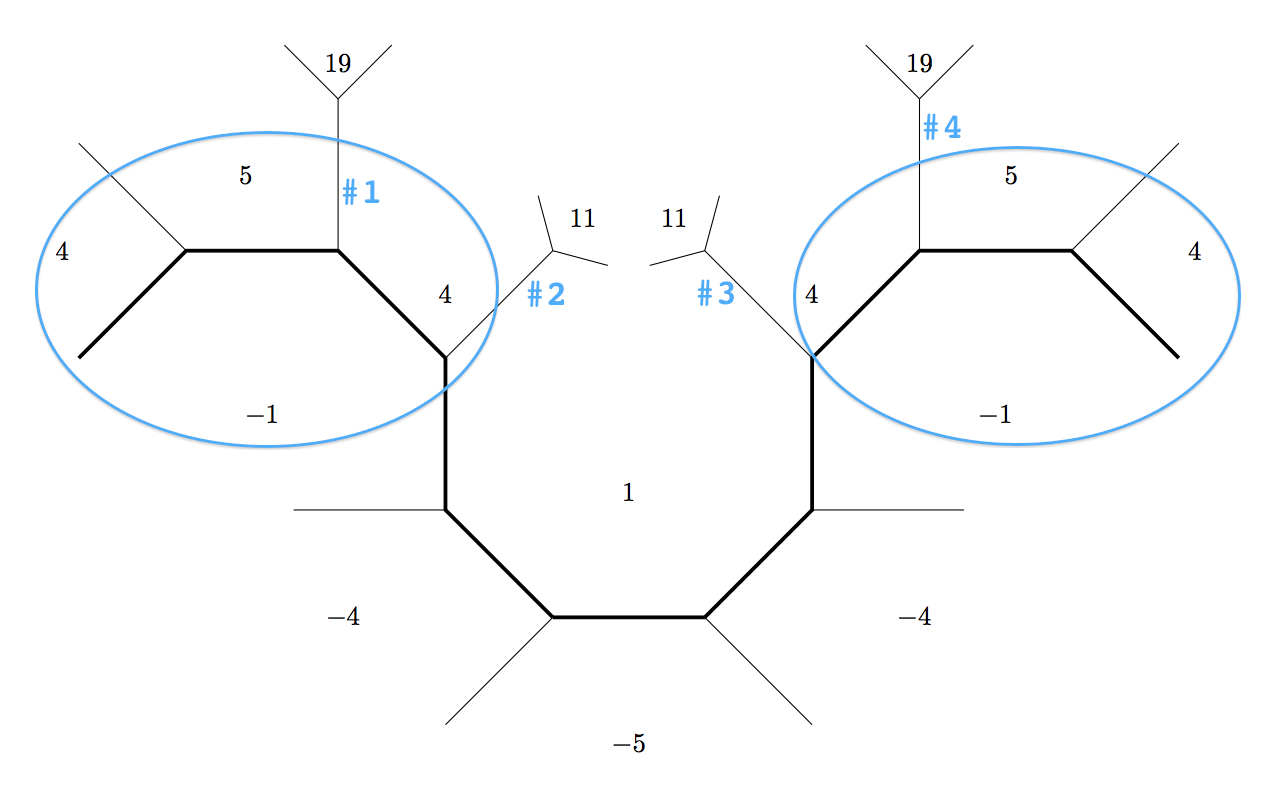
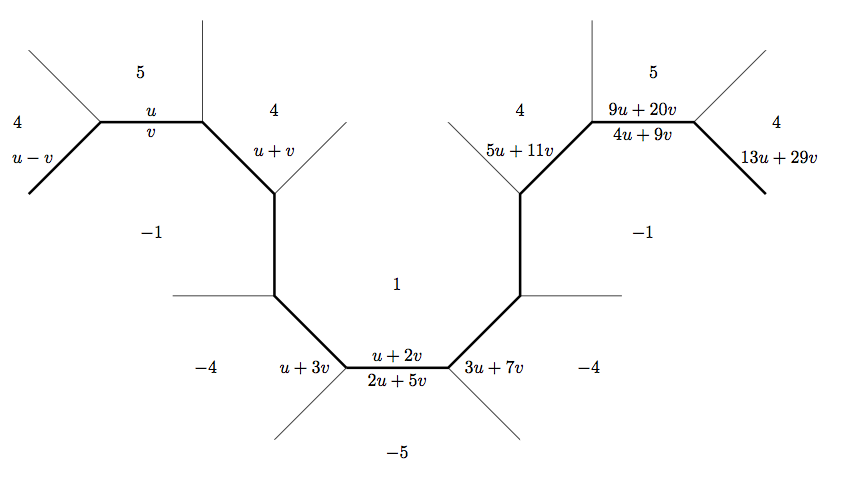
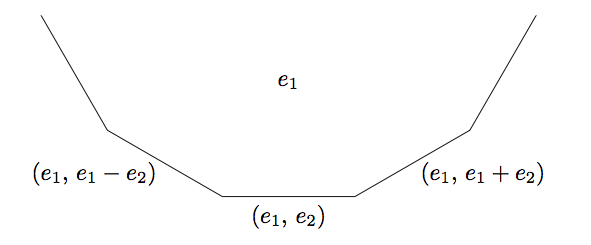
To answer the question \(5 x^2 - y^2 = 9\), we'll use the same pretty picture, but emphasize different parts of it. As you can see below, to classify all the values, we only need to travel from the initial base
along the river until we arrive at an identical base as the blue circles indicate below:
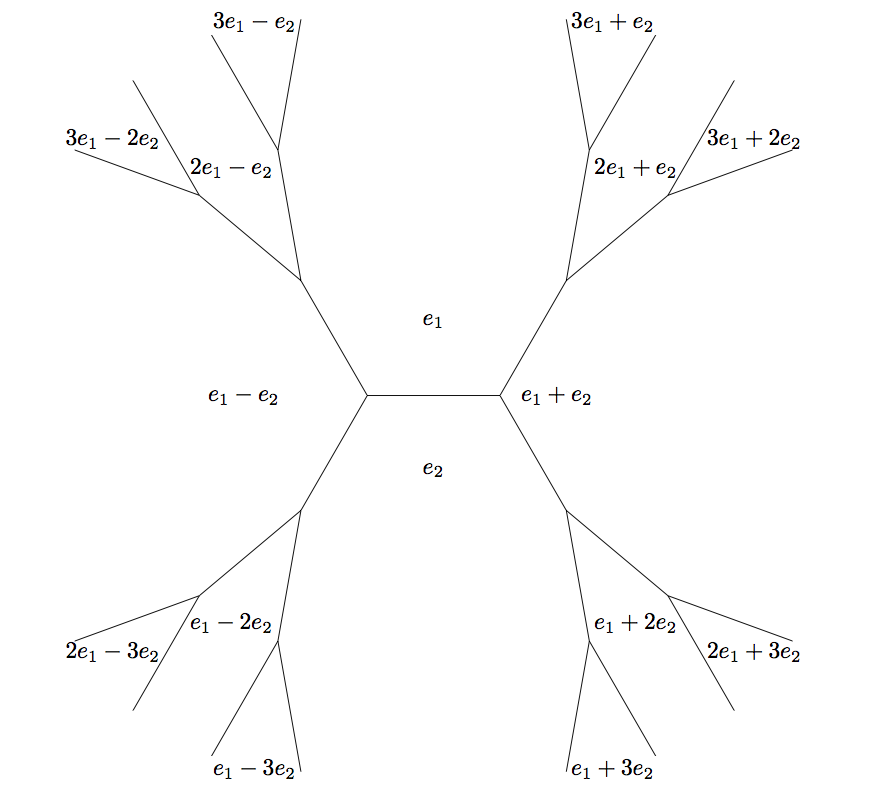
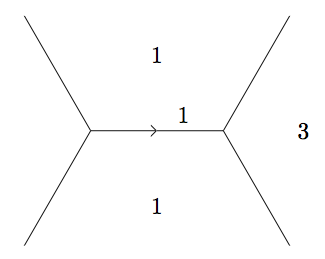
As noted above, for problem 137, we luckily were concerned about finding values \(4\) or \(1\), and the climbing lemma saved us from leaving the river. However, as I've noted above with #1, #2, #3, and #4, there are four tributaries coming from the river where we can consider larger values. Using the Arithmetic Progression Rule, we find values \(19\), \(11\), \(11\), and \(19\) as the first set of values above the river. From this point, we can stop checking for solutions to \(f(x, y) = 9\) since the climbing lemma says all further values above the tributaries will be \(11\) or greater. Thus, the only solutions come via scaling solutions of \(f(x, y) = 1\) by a factor of \(3\) (using homogeneity of a quadratic form).
Now for the (Python) code.
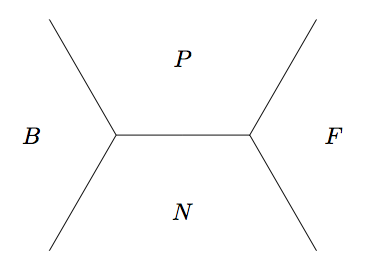
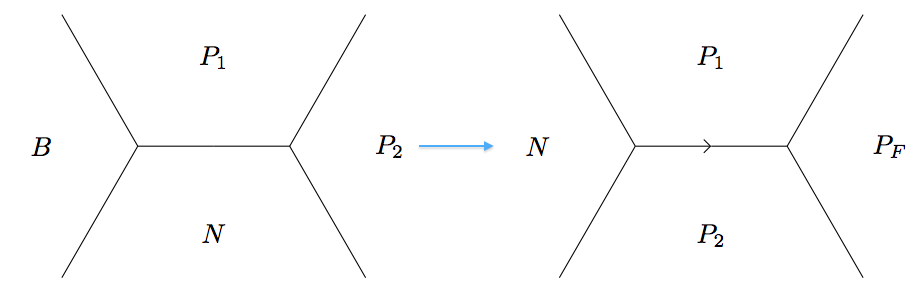
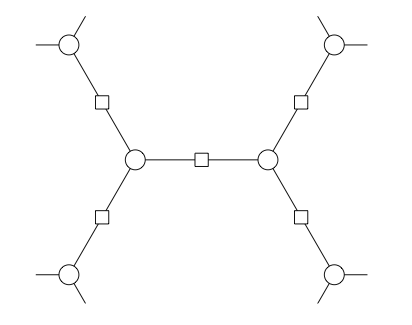
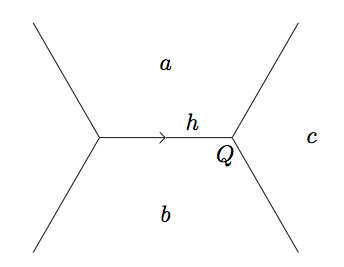
First, the data structure will be representative of a base along the river, but will also include the previous and next faces (on the shared superbases) and so we'll call it a juncture (my term, not Conway's). Each face in a juncture needs to be represented by both the pair \((x, y)\) and the value that \(f\) takes on this face. For our sanity, we organize a juncture as a tuple \((B, P, N, F)\), (in that order)
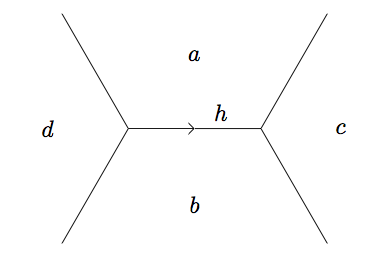
where \(P\) and \(N\) form a base straddling the river, with \(P\) taking the positive value and \(N\) negative, as well as \(B\) the face "back" according to our orientation and \(F\) the face "forward". Note, depending on the value of the form at \(F\), the river may "turn left" or "turn right" at the superbase formed by \(P\), \(N\) and \(F\).
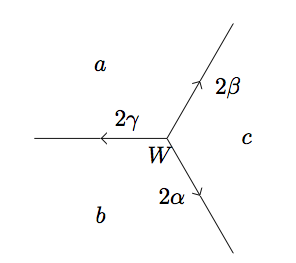
To move "along the river until we arrive at an identical base", we need a way to move "forward" (according to our imposed orientation) to the next juncture on the river. Moving along the river, we'll often come to superbases \((B, N, P)\) and need to calculate the forward face \(F\). To calculate \(F\), assume we have already written a plus function that determines the vector at \(F\) by adding the vectors from \(P\) and \(N\) and determines the value at \(F\) by using the arithmetic progression rule with the values at all three faces in the superbase. Using this helper function, we can define a way to get the next juncture by turning left or right:
def next_juncture_on_river(juncture):
B, P, N, F = juncture
forward_val = F[1]
if forward_val < 0:
# turn left
NEXT = plus(P, F, N[1])
return (N, P, F, NEXT)
elif forward_val > 0:
# turn right
NEXT = plus(N, F, P[1])
return (P, F, N, NEXT)
else:
raise Exception("No infinite river here.")
Next, to know when to stop crawling on the river, we need to know when we have returned to an identical juncture, so we define:
and crawl the river using the functions defined above. (Note: \(f(1, -1) = a(1)^2 + b(-1)^2 = a + b\), etc.)
To find the recurrence, we need just walk along the river until we get an identical juncture where the trivial base is replaced by the base \((p, q), (r, s)\). Using the same terminology as in part one, let the base vectors define a sequence \(\left\{(u_k, v_k)\right\}_{k \geq 0}\) with \(u_0 = (1, 0)\) and \(v_0 = (0, 1)\), then we have a recurrence \begin{align*}u_{k + 1} &= p u_k + q v_k \\ v_{k + 1} &= r u_k + s v_k. \end{align*} Using this -- \(u_{k + 2} - p u_{k + 1} - s(u_{k + 1} - p u_k) = q v_{k + 1} - s (q v_k) = q(r u_k)\) -- hence \(u\) satisfies the recurrence \(u_{k + 2} = (r q - p s)u_k + (p + s)u_{k + 1}\). (You can check that \(v\) satisfies this as well.) Hence our function to spit out the recurrence coefficients is:
and have the negative from across the river as the "back" face. With this definition, we first write a function to return all tributaries:
As far as Project Euler is concerned, in addition to Problem 137, I was able to write lightning fast solutions to Problem 66, Problem 94, Problem 100, Problem 138 and Problem 140 using tools based on the above -- a general purpose library for solving binary quadratic forms over integers!
def juncture_ident(juncture1, juncture2):
B1, P1, N1, F1 = juncture1
B2, P2, N2, F2 = juncture2
return ((B1[1] == B2[1]) and (P1[1] == P2[1]) and
(N1[1] == N2[1]) and (F1[1] == F2[1]))
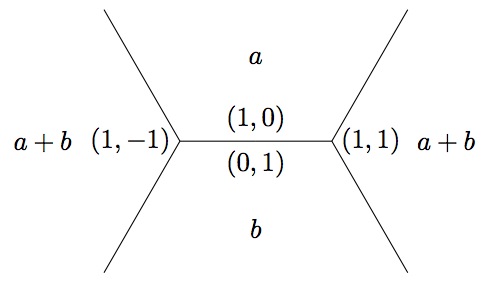
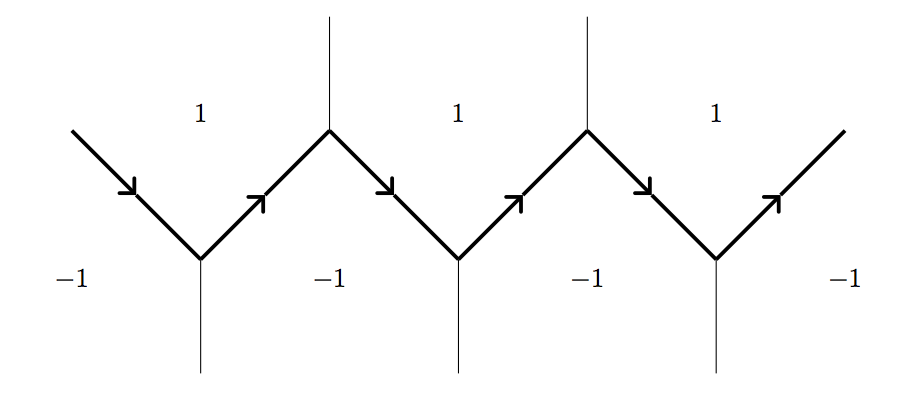
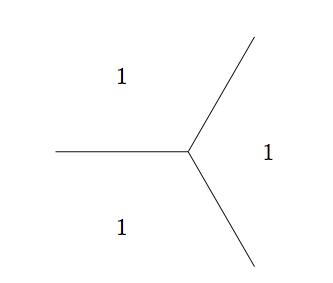
Using these functions, we can first find the recurrence that will take us from a base of solutions to all solutions and second, keep track of the positive faces on the river to generalize the solution of \(f(x, y) = z\). For both of these problems, we impose a simplification for the sake of illustration. We will only be considering quadratic forms \[f(x, y) = a x^2 + b y^2\] where \(a > 0\), \(b < 0\) and \(\sqrt{\left|\frac{a}{b}\right|}\) is not rational. This guarantees the existence of a river. We will pass such forms as an argument form=(a, b) to our functions. We start our river at the juncture defined by the trivial base \((1, 0), (0, 1)\)and crawl the river using the functions defined above. (Note: \(f(1, -1) = a(1)^2 + b(-1)^2 = a + b\), etc.)
To find the recurrence, we need just walk along the river until we get an identical juncture where the trivial base is replaced by the base \((p, q), (r, s)\). Using the same terminology as in part one, let the base vectors define a sequence \(\left\{(u_k, v_k)\right\}_{k \geq 0}\) with \(u_0 = (1, 0)\) and \(v_0 = (0, 1)\), then we have a recurrence \begin{align*}u_{k + 1} &= p u_k + q v_k \\ v_{k + 1} &= r u_k + s v_k. \end{align*} Using this -- \(u_{k + 2} - p u_{k + 1} - s(u_{k + 1} - p u_k) = q v_{k + 1} - s (q v_k) = q(r u_k)\) -- hence \(u\) satisfies the recurrence \(u_{k + 2} = (r q - p s)u_k + (p + s)u_{k + 1}\). (You can check that \(v\) satisfies this as well.) Hence our function to spit out the recurrence coefficients is:
def get_recurrence(form):
a, b = form
B = ((1, -1), a + b)
P = ((1, 0), a)
N = ((0, 1), b)
F = ((1, 1), a + b)
J_init = (B, P, N, F)
J_curr = next_juncture_on_river(J_init)
while not juncture_ident(J_init, J_curr):
J_curr = next_juncture_on_river(J_curr)
final_B, final_P, final_N, final_F = J_curr
p, q = final_P[0]
r, s = final_N[0]
return (r*q - p*s, p + s)
For solving \(f(x, y) = z\), (\(z\) positive) we need to consider all the positive tributaries coming out of the river and let them grow and grow until the climbing lemma tells us we no longer need to consider values larger than \(z\). In order to consider tributaries, we describe a new kind of juncture. Instead of having a positive/negative base in the center of the juncture, we have two consecutive faces from the positive sideand have the negative from across the river as the "back" face. With this definition, we first write a function to return all tributaries:
def all_positive_tributaries(form):
# ...Initialization logic...
new_positives = []
J_curr = next_juncture_on_river(J_init)
while not juncture_ident(J_init, J_curr):
# we add a new positive if the forward
# value is positive
forward = J_curr[-1]
if forward[1] > 0:
new_positives.append(J_curr)
J_curr = next_juncture_on_river(J_curr)
# For each (B, P, N, F) in new_positives, we want to
# transform to a juncture with positive values, which will
# be (N, P_1, P_2, P_F)
result = []
for new_positive in new_positives:
B, P, N, F = new_positive
new_face = plus(P, F, N[1])
tributary = (N, P, F, new_face)
result.append(tributary)
return result
For each tributary, we can climb up away from the river until our values are too large. So we write a helper function to take a given tributary and a max value and recursively "climb" the topograph until we exceed the value. This function will naively return all possible faces (value and vector) without checking the actual values.def seek_up_to_val(juncture, max_value):
N, P_1, P_2, P_F = juncture
if P_F[1] > max_value:
return []
result = [P_F]
turn_left = plus(P_1, P_F, P_2[1])
J_left = (P_2, P_F, P_1, turn_left)
result.extend(seek_up_to_val(J_left, max_value))
turn_right = plus(P_2, P_F, P_1[1])
J_right = (P_1, P_F, P_2, turn_right)
result.extend(seek_up_to_val(J_right, max_value))
return result
Finally, we can combine these two helper functions into a function which will find all solutions to \(f(x, y) = z\) above the river. We may have a pair (or pairs) \((x, y)\) on the topograph where \(f(x, y) = \frac{z}{k^2}\) for some integer \(k\); if so, this gives rise to a solution \((kx, ky)\) which we'll be sure to account for in our function.def all_values_on_form(form, value):
# Use a helper (factors) to get all positive integer factors of value
factor_list = factors(value)
# Use another helper (is_square) to determine which factors can be
# written as value/k^2 for some integer k
valid_factors = [factor for factor in factor_list
if is_square(value/factor)]
tributaries = all_positive_tributaries(form)
found = set()
for tributary in tributaries:
candidates = seek_up_to_val(tributary, value)
found.update([candidate for candidate in candidates
if candidate[1] in valid_factors])
# Since each tributary is of the form (N, P_1, P_2, P_F) for
# P_1, P_2 on the river, we need only consider P_1 and P_2 since
# those faces above are in candidates. But P_2 will always be in
# next tributary, so we need not count it. You may assume this ignores
# the very final tributary, but here P_2 actually lies in the
# second period of the river
N, P_1, P_2, F = tributary
if P_1[1] in valid_factors:
found.add(P_1)
# Finally we must scale up factors to account for
# the reduction by a square multiple
result = []
for face in found:
(x, y), val = face
if val < value:
ratio = int(sqrt(value/val))
x *= ratio
y *= ratio
result.append((x, y))
return result
Combining all_values_on_form with get_recurrence, we can parameterize every existing solution!As far as Project Euler is concerned, in addition to Problem 137, I was able to write lightning fast solutions to Problem 66, Problem 94, Problem 100, Problem 138 and Problem 140 using tools based on the above -- a general purpose library for solving binary quadratic forms over integers!